公式は便利だが…

３年生には、最後の計算チェックとして、因数分解を解かせています。

２年生には、先に進んでいる生徒には、因数分解の練習をしてもらっています。

そのため、「因数分解」に接する機会が多いのですが、その中で感じるのが

「『共通因数』を使った因数分解ができないな…」

ということです。

公式のインパクトが強すぎて…

「『共通因数』を使った因数分解」

とは、たとえば

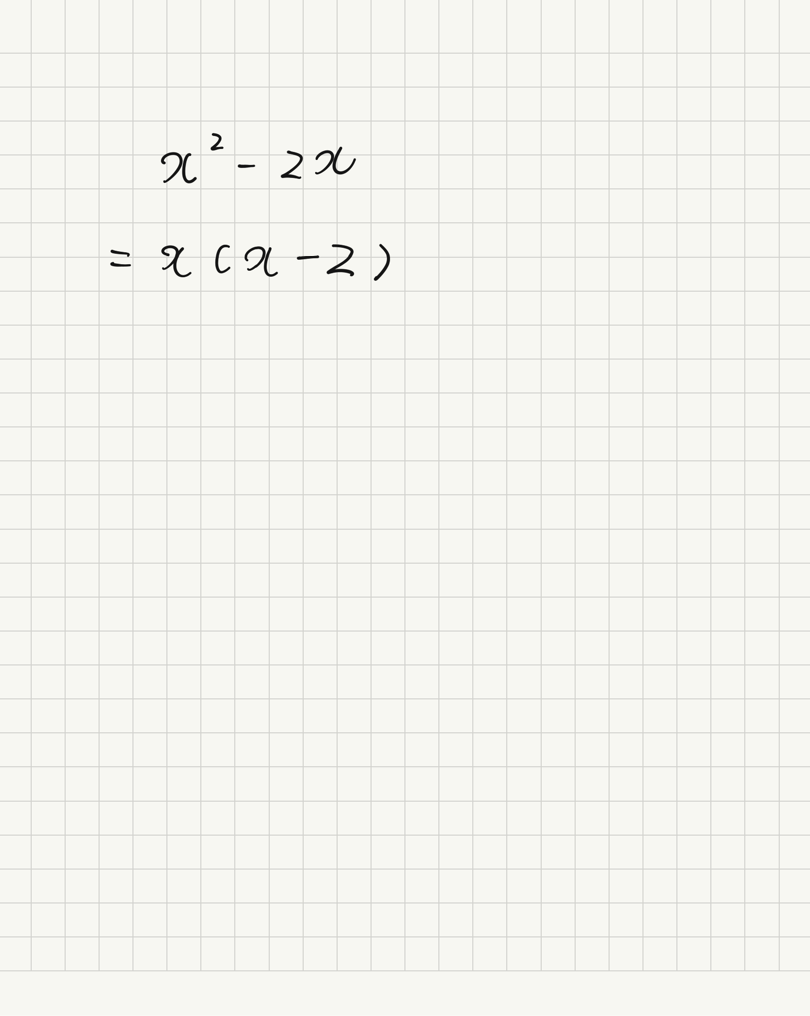
のように、２つの項に共通している因数「ｘ」をカッコの外に出す因数分解のことを言います。

それほど難しい計算ではないと思うのですが、これが予想以上にできない。

受験直前の中３生でも、いまだに間違えているので、思わずため息をついてしまいます。

因数分解というと、「乗法公式」を使ったものが一般的です。

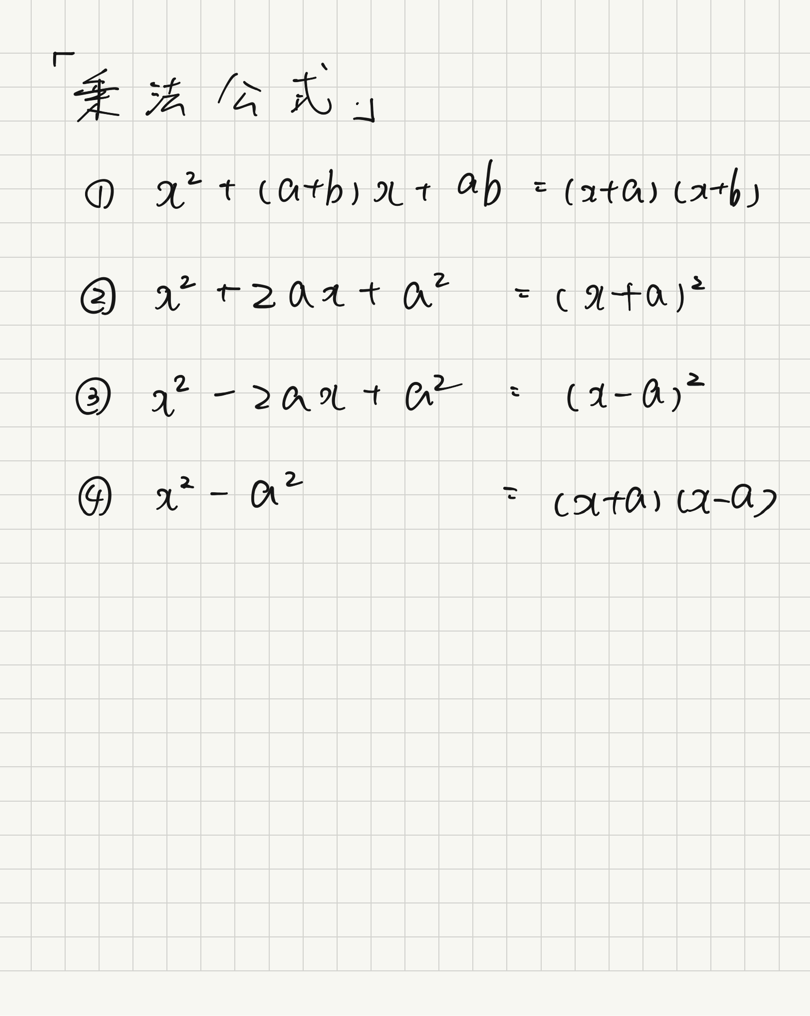
「乗法公式」が覚えられていないと、中３の数学は進められません。

なので、必死に覚えてもらいます。

その印象が強いせいか、「因数分解＝乗法公式」というふうに考えてしまい、「共通因数を使った因数分解」に気づくことができない生徒が非常に多くて困ります。

「公式」を覚えることは大事だが…

「公式」は便利ですし、覚えることは大事です。

ですが、その一方で、

「公式さえを覚えておけばいい」

と、安直に考えてしまう子が多いのも、考えものです。

特に「理科」を指導していると、そのことを感じます。

ある程度問題が解けるようになってきたら、

「なぜ、そのような公式になるのか？」
「その公式の計算をしたら、どのようなことを知ることができるのか？」

という部分を、もう少し自分なりに考えてもらいたいな、と思います。

例えば、「密度」の公式です。

「密度＝質量÷体積」

で求められますが、ではこの計算から、何を求めることができるのか。

「質量」を「体積」で割ることで、

「１立法センチメートルあたりの質量」

を出すことができる。

つまり、「密度」というのは「単位量」についての考え方を使っている。

ある程度実力のある生徒は、このあたりまで掘り下げて、理解するようにしておいてほしいです。

私の話で恐縮ですが、私は公式（特に理科の公式）を覚えるのがあまり好きではありませんでした。

中学時代、理科の先生とは色々とあったため、「言われた通りにやるのが嫌だった」という個人的な事情がありました。

教える立場からすると、非常に面倒な生徒だったと思います。

ですが、

「なぜ、このような公式があるのだろう？」
「この公式から、どのようなことが言えるのだろう？」

ということは、常に考えていました。

なので、「公式」自体を忘れてしまっても、

「密度は単位量を求めればいいのだから、質量を体積で割ればいいんだな」

と思って、計算できていました。

「こっちの方がめんどくさい」

と思うかもしれません。

ですが、「表面的な」公式を覚えても、すぐに忘れますが、こうした「本質的な理解」ができていれば、時間が経っても忘れることはありません。

また、このような「本質的な部分を理解する」ところに、「勉強の面白さ」があると感じています。

なので、ある程度実力のある生徒には、このあたりの話をするのですが、安易な「公式」に走ってしまう生徒がほとんどです。

その点に、少し不満を感じています。

「本質的な理解」を

「小学校の算数が重要」と繰り返し言っているのも、結局この「本質的な理解」をするためには、「小学校の算数」が土台になるからです。

先程の例に挙げた「単位量あたり」の考え方は、小学校の算数でやります。

「小学校の算数」が、表面的な理解しかできていないので、中学の数学や理科が理解できず、「公式」に頼ることになってしまっている。

そうした現状に寂しさを感じます。

なので、小学生で、ある程度の実力のあるお子さんには、ただ、「テストの点数」を追求するのではなく、「本質的な理解」をするような勉強をしておいてほしい。

そう思っています。

※猿田塾へのお問い合わせは、こちらから