
「数直線」でわかる、算数の学力
2024/2/7
根が深い「文章題が解けない」
最近読んだこちらの本

「算数の文章題が解けない」原因を探る内容になっています。
一口に「文章題が解けない」と言いますが、その原因はじつは根深い。
多くの方が「文章が読み取れない」から、文章題が解けない、という風に考えています。
ですが、詳しく分析してみると、
「そもそも算数の基礎的な考え方が、きちんと身についていない」
ことが原因である場合の方が多いです。
その中で、「確かに」と思う内容がありました。
数直線
それは「数直線」を使った問題でした。
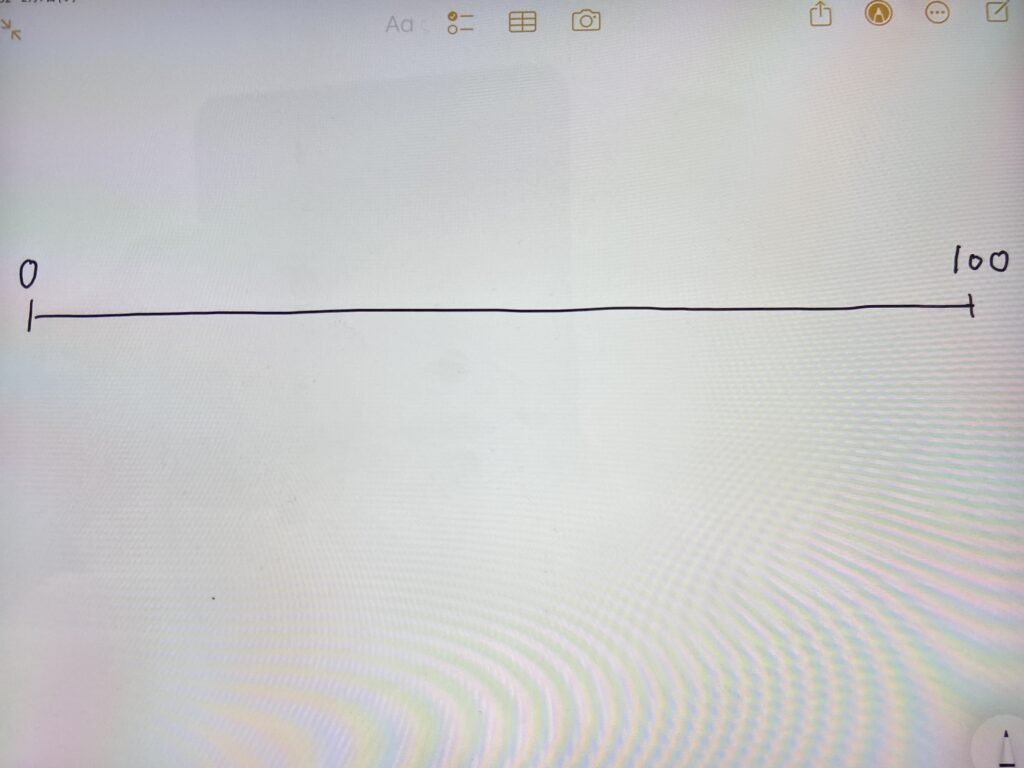
このような「0~100」を表す数直線があります。
ここに「4」「18」「23」「71」といった数字を、矢印で表す問題を出した時、様々な間違えが出てきたそうです。
例えば「23」という数字。
きちんと答えられた生徒は、数直線を4つに分割し、「25」よりも少し小さい位置を指す、という風に答えられました。
ところが、間違えた生徒は
・線を縦に23本引いて答える
・「23mm」を定規で測って答える
という答え方をしていたそうです。
また、「71」という数字を表す場合、数直線の長さが71mmで足りない場合、「17mm」のところに答えていた子もいたそうです。
数の「相対性」が理解できない
この「数直線」を使った問題で間違える生徒は、「数の相対性」が理解できていない、と言えます。
数字といえば「絶対的」なものしか表すことがない。
そのため「場面」によって、数字の意味が変わってくる、ということが理解できない。
そしてこのような子どもの数は、大人が思っている以上に多い。
そう感じています。
数の「絶対性」についての感覚は、比較的早い段階で、子どもたちは自然と身につけていくようです。
ですが、数の「相対性」については、練習して身につけていく必要がある。
ここがきちんとわからないと、「分数」の考え方が理解できません。
なので、「数の相対性」が身についていない子は
「1/2と1/3の大小関係」を聞かれた時に、
「3という大きい数字が使われているから」
という理由で、「1/3」と答えてしまう。
そうなってしまうのだと思います。
「家庭学習」が重要
生徒を指導していても、この「数の相対性」を正しく理解できている生徒が、思った以上に少ないことを感じます。
ここがきちんと理解、習得できていないので、小5になって「割合」を学ぶと、途端に「?」となる生徒が続出するのだと思います。
「数の相対性」を学ぶには、小さいうちに数字の「絶対性」だけでなく、「相対性」を感覚的に理解していく必要があります。
この部分は、
「学校や塾で、座学で教える」
というだけでは、身につかないように感じています。
頭では理解できても、感覚として理解し、使いこなすことができない。
感覚として理解していくには、日頃の生活の中で、体験を通じて理解していく。
それができるのは「ご家庭」しかないのかな、という気がしています。
ですので、小学校で分数を習い始める小2の終わり頃から
「数の相対性」
といったものを意識して伝えていっていただけると、算数でのつまづきが減らせるのではないか。
そう思っています。
※猿田塾へのお問い合わせは、こちらから